Laboratory of Biological Modelling
George N. Reeke, Jr.
Associate Professor
 Interest centers on the nervous system, which provides the biological substrate for behavior and higher thought processes. Models are being constructed that attempt to provide a conceptual bridge between the physical phenomena occurring in the nervous system and the psychological level. A technique called synthetic neural modelling is used to construct computer-simulated brain regions or entire organisms with senses, motor outputs, and a nervous system. Neurons in these models have biologically realistic properties based on experimental neurophysiology. They interact with each other and with the environment according to a comprehensive Darwinian view of population dynamics in the nervous system proposed by G. M. Edelman.
Interest centers on the nervous system, which provides the biological substrate for behavior and higher thought processes. Models are being constructed that attempt to provide a conceptual bridge between the physical phenomena occurring in the nervous system and the psychological level. A technique called synthetic neural modelling is used to construct computer-simulated brain regions or entire organisms with senses, motor outputs, and a nervous system. Neurons in these models have biologically realistic properties based on experimental neurophysiology. They interact with each other and with the environment according to a comprehensive Darwinian view of population dynamics in the nervous system proposed by G. M. Edelman.
The ability of the model organisms to display adaptive behavior has been tested both in simulated worlds and in the real world, under conditions of both normal and impaired nervous system function. These models have shown how the ability to recognize objects and events in the environment can arise in the developing nervous system as a result of the operation of selective processes guided by innate value systems. There is no need for built-in representational codes or computational algorithms, nor for feedback of error signals from omniscient external teachers. These results call into question the popular theory that the brain is a kind of computer.
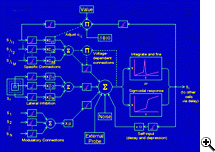
 Areas of particular interest for exploration by synthetic modelling include sensory integration, perceptual categorization, control of locomotion, and aspects of memory. Current work focuses on neural mechanisms for recognition and recall of temporal patterns, which are of fundamental importance for language and music. To increase the realism of network simulations we have developed a composite approach to modelling neurons. In this approach, precalculated curves are used to model the time course of stereotypical responses, such as that of the fast sodium conductance, while a fuller treatment is used to model conductances whose responses are more dependent on instantaneous conditions in the the cell. Composite models are more realistic than simple "integrate-and-fire" models, yet can be simulated in a computer much more rapidly than full Hodgkin-Huxley models. We have employed this approach to explore the discharge responses of a model cerebellar Purkinje neuron to excitatory activation that exhibited a range of temporal correlations. We have also modeled mechanisms for "top-down" (i.e. attentional) modulation of responses in V1 visual cortex, mechanisms of song learning in oscine birds, and effects of GABAergic anesthetic agents on cortical network activity.
Areas of particular interest for exploration by synthetic modelling include sensory integration, perceptual categorization, control of locomotion, and aspects of memory. Current work focuses on neural mechanisms for recognition and recall of temporal patterns, which are of fundamental importance for language and music. To increase the realism of network simulations we have developed a composite approach to modelling neurons. In this approach, precalculated curves are used to model the time course of stereotypical responses, such as that of the fast sodium conductance, while a fuller treatment is used to model conductances whose responses are more dependent on instantaneous conditions in the the cell. Composite models are more realistic than simple "integrate-and-fire" models, yet can be simulated in a computer much more rapidly than full Hodgkin-Huxley models. We have employed this approach to explore the discharge responses of a model cerebellar Purkinje neuron to excitatory activation that exhibited a range of temporal correlations. We have also modeled mechanisms for "top-down" (i.e. attentional) modulation of responses in V1 visual cortex, mechanisms of song learning in oscine birds, and effects of GABAergic anesthetic agents on cortical network activity.
Neural Spike Train Entropy In principle, and neglecting changes in membrane potential that are probably not significant, neurons can respond to just the rate at which spikes are received from some other neuron, or to the specific temporal pattern in which those spikes are received. (Because there is no clock in the brain, it is actually the intervals between spikes, or interspike intervals, not the absolute spike times, that are significant.) It is not currently clear by which cells and under which conditions one or the other coding method is used in the nervous system. To study this question, it is important to be able to measure the information that can be conveyed from one cell to another by one or another of these methods. By analogy with electronic information transfer systems, such information corresponds to the entropy of the signal and is measured in bits. The information transmitted by a rate code is easily derived, but in the case of a spike-time code, the entropy depends on the time resolution with
In principle, and neglecting changes in membrane potential that are probably not significant, neurons can respond to just the rate at which spikes are received from some other neuron, or to the specific temporal pattern in which those spikes are received. (Because there is no clock in the brain, it is actually the intervals between spikes, or interspike intervals, not the absolute spike times, that are significant.) It is not currently clear by which cells and under which conditions one or the other coding method is used in the nervous system. To study this question, it is important to be able to measure the information that can be conveyed from one cell to another by one or another of these methods. By analogy with electronic information transfer systems, such information corresponds to the entropy of the signal and is measured in bits. The information transmitted by a rate code is easily derived, but in the case of a spike-time code, the entropy depends on the time resolution with
which a recipient cell can process the spike signal and may be reduced by correlations between successive spike intervals.
Our lab has been interested for some time in this problem of measuring spike train entropy. Our most recent contribution is what we have called the "history clustering" method because it detects and takes into account clusters of spikes with similar interval histories. A paper describing the history clustering method and giving examples of its use is at this writing in press in the journal Neural Computation. The method is implemented in Matlab code but uses C-language "mex" functions to compute the multidimensional Kolmogorov-Smirnov statistic (MDKSS) that is central to the history clustering method, as well as the Strong et al. method of entropy calculation that is included in the package for comparison (reference in the readme file included with the code). The Matlab and Strong et al. mex code along with a demonstration script, test data, and sample results are available on our "downloads" page for general use under terms of the GPL open source license. The code is provided in both .tgz format for Linux users and .zip for Windows users. Included is a README file that describes the usage, literature references, and revision history of the package. It is necessary first to download the MDKSS package (see next section) and compile the code found there using the "make" file provide in order to make the MDKSS code available to the history clustering entropy package.
If you use the software, please send your name and email address to reeke@mail.rockefeller.edu. I will use this information to send you notification of any future updates. I would also like to know a little about what you are using the programs for and any suggestions for improvements. It is not required that you do this.
Multidimensional Kolmogorov-Smirnov Statistic
The rate-limiting calculation in the history-clustering entropy estimation method is the determination of parameters for generation of an artifiicial data set that is statistically indistinguishable from the experimental data under test but for which the entropy can be calculated analytically. For this purpose, we use a multidimensional version of the well known Kolmogorov-Smirnov test for comparing two distributions. The multidimensional version was proposed by G. Fasano & A. Franceschini, "A multidimensional version of the Kolmogorov-Smirnov test," Monthly Notices of the Royal Astronomical Society, 225:155-170 (1987). An algorithm devised by G.N. Reeke and described fully in the readme file accompaying the package is used here. In this algorithm, the data space is divided into a recursively subdivided hierarchy of rectilinear bricks. The count of points in a brick can be used when a brick lies entirely in one hyperquadrant relative to a point under test, minimizing the need to check the coordinates of each point individually. The code is generally faster than the obvious brute-force algorithm (code also suplied) only for dimensions 2, 3, and 4, but these are perhaps the most common cases in practice. The computation makes use of a work area that is allocated in a separate call. The work area may be reused for multiple calculations with the same dimensional parameters. The code is written in C and can be used wih either single- or double-precision floating-point data. "make" files are provided to compile the code either as a library of functions callable from other C or C++ code, or as "mex" functions callable from Matlab code.
The code is provided under the GPL open source license. It may be downloaded from our "downloads" page or directly as a .tgz file from here or as a .zip file from here. If you use the software, please send your name and email address to reeke@mail.rockefeller.edu. I will use this information to send you notification of any future updates. I would also like to know a little about what you are using the programs for, especially if for some use other than as a componnt of the history clustering entropy package, and any suggestions for improvements. It is not required that you do this.